

From there decide what spin is needed and drop down into the shot. While standing at the table, aim as if using a centre ball hit. You may be thinking that his technique only works with a centre ball hit, but it’s easy to adapt it to using different spin. You are already visualizing the angle of entry into the rail so the exit angle will be the same on a plain ball shot. Not only this, since you are focusing on the point you will hit on the rail, you will be more precise playing position off that rail. Using multiple points of reference takes a lot of the guesswork out of potting balls. So rather than focus on a point on the object ball, we can just imagine sending the cueball to one of those points on the rail, depending on which direction you are cutting the ball. Even if you can’t see the pocket when your down on the shot, you will be able to see one of those contact points. This gives you multiple points of reference for the shot and at least one is always in your line of vision.įor example, in the shot above, you can see the tangent line extend into 2 points on the rail. The triangle always extends into two rails. Shoot the shot in such a way that the cue ball, with no spin, would travel down that line and the pot is guaranteed.įor any given object ball position, the tangent line will form a triangle on the table that will be the same no matter where the cue ball is. Instead, we can imagine the tangent line (the black line) if the pot was successful. This problem is compounded the further the object ball is from the pocket. You could visualize a line from the ball to the pocket (the green line), but this is out of your line of sight once you’re down on the shot, making it difficult to judge. The tangent line is sometimes easier to see than the shot line.
#Tangent line how to
This article shows you how to use this fact to aim.
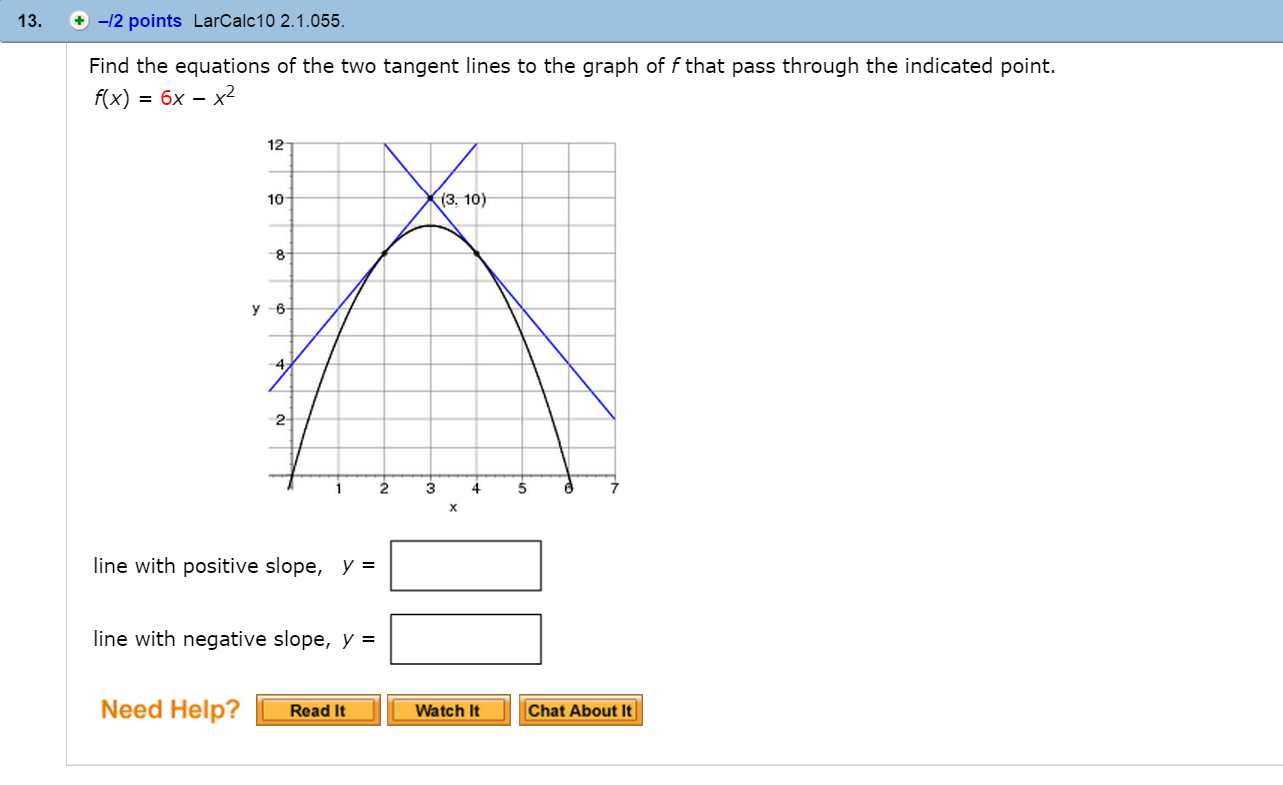
The basic gist of it is, when the cue ball is sliding and hits an object ball, it always separates at 90 degrees from the cut angle. It is crucial for playing position and the rest of this article won’t make much sense if you don’t know how to use it. If you’re not familiar with the tangent line, read about it here. This is much simpler than trying to find a contact point on a sphere and has the added bonus of improving your positional play. Instead of focusing on where to hit the object ball, we are going to focus on where the cue ball will go if the shot is made using the tangent line. What most of them have in common is that they focus on the contact point on the object ball and aiming different parts of the cue or cue ball at it. Cohn-Vossen, "Geometry and the imagination", Chelsea (1952) (Translated from German) MR00466.The internet is littered with various “aiming systems” and methods to visualize the line of the shot. Gostiaux, "Differential geometry: manifolds, curves, and surfaces", Springer (1988) (Translated from French) MR09174.53001 The equation of the tangent to a curve $\vect, \quadīy a tangent to a surface $S$ at a point $M$ one means a straight line passing through $M$ and lying in the tangent plane to $S$ at $M$.
If a curve in the plane with rectangular coordinates is defined by the equation $y=f(x)$ and $f$ is differentiable at the point $x_0$, then the slope of the tangent at $M$ is equal to the value of the derivative $f^\prime(x_0)$ at $x_0$ the equation of the tangent at this point has the form Not every continuous curve has a tangent, since $MM_1$ need not tend to a limiting position at all, or it may tend to two distinct limiting positions as $M_1$ tends to $M$ from different sides of $L$ ( Fig. 2). A curve $L$ and point $M$ on it without a tangent ( pdf)


 0 kommentar(er)
0 kommentar(er)
